MARZO

Vector Tangente y Normal 

La tangente de una curva es una recta que intersecta la curva en un solo punto. Es conocido por nosotros a través del cálculo que mediante la diferenciación de una función se obtiene el punto tangencial para la curva de esa función. Un concepto similar es aplicable al cálculo vectorial, junto con una excepción.

Para una función con un vector de la forma, (x), un vector de la forma es llamado vector tangente en el caso de que esta función sea real y su magnitud no sea igual a cero. En esta situación, la tangente de la función dada (x) en un punto arbitrario es paralela al vector tangente, en ese punto. Aquí, con el fin de tener un vector tangente, 0 es un pre-requisito esencial. Esto es debido a que un vector de magnitud cero no puede tener dirección.

De manera similar, un vector tangencial unitario es definido como,

Aquí s es la longitud total del arco dado, (t) es el vector posición de la función dada y t es la variable de parametrización.

En la figura anterior, X es un punto estático, mientras que P es un punto en movimiento. El punto P se mueve lentamente en la dirección del punto X, mientras el punto P se acerca al punto X, el vector desde el punto X hasta el punto P se acerca al vector tangente en el punto X. La recta que contiene el vector tangente se conoce como recta tangencial.

Un vector normal es algo similar a un vector unitario, suponga que para una función (x), (t) es el vector posición, entonces el vector normal para la función dada es definida como,

En cada punto de una curva, el plano osculador es el plano que contiene a su vector tangente y al vector normal a la curva. Para una partícula desplazándose en el espacio tridimiensional, el plano osculador coincide con el plano que en cada instante contiene a la aceleración y la velocidad. La ecuación de este plano viene dada por:

Donde:

, el punto de la trayectoria.

, el vector velocidad en el punto considerado.

, las coordenadas de un punto genérico del plano osculador.

Si se tiene una partícula en la posición , moviéndose con velocidad  y sometida a una aceleración  el plano osculador viene dado por el conjunto de puntos:

Obviamente si la partícula tiene un movimiento rectilíneo el plano osculador no está definido.

Triedro Móvil

Sea r=r(s) con s Є I una parametrización natural de una curva C de clase C³. Como s es un parámetro longitud de arco se tiene

En cada punto de la curva C donde r''(s)≠0 están definidos los tres vectores siguientes

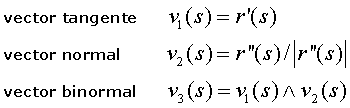
El sistema de vectores anterior es ortonormal y se denomina triedro móvil de Frenet. Asociados a cada uno de los vectores del triedro móvil tenemos una recta y un plano:

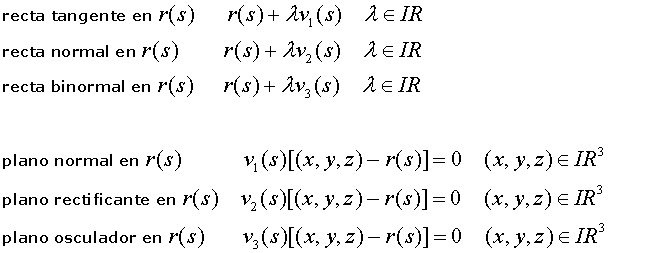
El triedro móvil se encuentra definido sólo en aquellos puntos en los que r''(s)≠0. Si este vector es nulo en un conjunto discreto de puntos de la curva, entonces la curva queda dividida por estos puntos en arcos en los que sí se tendrá triedro móvil. Las curvas para las que  r''(s)≠0 en un intervalo serán, en dicho intervalo, un segmento de recta. 

Curvatura y torsión

Definición Se denomina curvatura de una curva C en un punto r(s) siendo s un parámetro longitud de arco a

Intuitivamente la curvatura mide lo que se le falta a la curva para ser una recta en cada punto.

Definición Se denomina torsión de una curva C en un punto r(s) siendo s un parámetro longitud de arco a

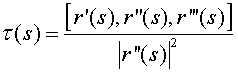
Intuitivamente, la torsión mide lo que le falta a la curva para estar contenida en un plano, es decir, para ser una curva plana.

Para un parámetro arbitrario t se tiene

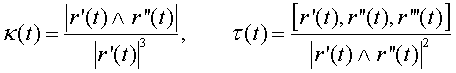
Teorema Es condición necesaria y suficiente para que una curva sea una recta que la curvatura sea idénticamente nula.

Teorema Es condición necesaria y suficiente para que una curva no rectilínea sea plana que la torsión sea idénticamente nula.

Función de dos variables

Una función de dos variables es una regla de correspondencia que asigna a cada pareja de números reales (x, y) un y sólo un número real z.

El conjunto de parejas ordenadas para las cuales la regla de correspondencia dá un número real se llama dominio de la función. El conjunto de valores z que corresponden a los pares ordenados se llama imagen o contradominio.

Una función de dos variables se denota usualmente con la notación

z = f (x, y)

Las variables x, y se llaman variables independientes, y z se llama variable dependiente.

La gráfica de una función de dos variables es el conjunto de puntos con coordenadas (x, y, z) en donde (x, y) está en el dominio de f y z = f (x, y).

Este conjunto de puntos forma una superficie en el espacio tridimensional.

En consecuencia, la grafica de una función f de dos variables es una superficie que consta de todos los puntos del espacio tridimensional cuyas coordenadas cartesianas están determinadas por las ternas ordenadas de números reales (x, y, z). Como el dominio de f es un conjunto de puntos del plano x, y, y puesto que cada par ordenado (x, y) del dominio de f corresponde a solo un valor de z, ninguna recta perpendicular al plano x,y puede intersectar a la grafica de f en mas de un punto.

Ejemplo ilustrativo 1

La función f del ejemplo 1 es el conjunto de todos los pares ordenados de la forma (P, z) tales que

 z=v25- x2 -y2

Por tanto, la grafica de f es la semiesfera en el plano x y por arriba de este cuyo centro es el origen y tiene radio 5. Esta semiesfera se muestra en la figura 1.